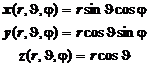Введение в теорию атома
Введение в теорию атома. Краткие математические сведения о сферических системах. Ротатор. Уравнение Шрёдингера для одноэлектронного атома (атом водорода и водородоподобные ионы).
8.1. Краткое содержание.
Шаровые координаты (r, J, j). Элемент объёма. Лапласиан в шаровых координатах. Уравнение Лапласа в сферических переменных. Роль симметрии в выборе радиальной части общего решения. Угловая часть уравнения Лапласа - уравнение Лежандра. Оператор момента импульса, его квадрат в шаровых переменных и его связь с уравнением Лежандра. Ротатор. Квантование модуля момента импульса ротатора. Операторные уравнения для момента импульса и их связь с уравнением Лежандра.
Уравнение Шрёдингера для электрона в атоме водорода. Разделение переменных. Радиальная и угловая части уравнения Шрёдингера и вид общего решения. Квантование модуля и проекций момента импульса электронного вращения вокруг ядра. Квантование энергии и энергетические уровни. Пределы изменения квантовых чисел. Боровский радиус и его вероятностный смысл.
Одноэлектронный гамильтониан в шаровых координатах и уравнение Шрёдингера для атома водорода (или водородоподобного иона). Разделение переменных. Атомные орбитали, их радиальные и угловые компоненты:
.
Квантовые числа (n,l,m), их взаимосвязь, пределы изменения и физический смысл. Квантование энергии, модуля и проекций момента импульса электрона на атомных орбиталях. Полярные диаграммы угловых компонент АО.
Раздел в значительной степени предназначен для начинающего читателя и одна из его целей – упражнения в элементарной алгебре линейных операторов.
8.2
. Предварительная общая информация.
Сферические переменные. Уравнение Лапласа. Атом водорода. Уравнение Шрёдингера. Разделение переменных (иллюстрации и основные формулы) Радиальная переменная r, азимутальная переменная (угол широты) J, переменная широты (угол широты) j . Квантовые числа.
|
Радиальная переменная r
Угол широты
J
Угол долготы
Декартовы координаты:
|
Интервалы изменения шаровых переменных: 0<r<¥; 0<J<; 0<j<2
Интервалы изменения переменных дают возможность выявить вид полярных диаграмм угловых функций - решений операторных уравнений.
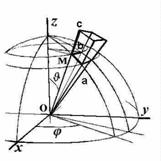
Элемент объёма в шаровых переменных (см. рис.):
8.3 Лапласиан.
Важное свойство лапласиана состоит в его симметрия ко взаимным перестановкам декартовых координат. Из этого свойства вытекают и приёмы решения наиболее распространённых дифференциальных уравнений в частных производных с его участием.
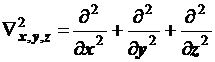. (8.2)
Простейшее дифференциальное уравнение в частных производных второго порядка, в котором лапласиан играет основную роль - уравнение Лапласа. В шаровых координатах лапласиан оказывается составленным из трёх независимых компонент-операторов, каждый из которых преобразует лишь одну из трёх независимых пространственных переменных.
Симметрией конкретной системы предопределяется выбор координат, в которых следует выразить лапласиан, ею определяется вид решений дифференциальных уравнений, в которых уравнение Лапласа оказывается в роли однородной части.
Таковы две задачи о сферически симметричных движениях.
Первая из них о свободном вращении без потенциальной энергии.
Вторая о вращении в поле центральной силы.
Основная квантово-механическая модель, применяемая для исследования сферического вращения как с потенциальной энергией, так и без неё, называется РОТАТОР.
Первая задача о стационарном вращении частиц с линейно распределённой массой относительно центра масс. Таковы все двухатомные молекулы, а также некоторые трёхатомные молекулы, такие как CO2
, CS2
. Эта задача более проста, и в ней вращение частицы свободное, т.е. совершается без потенциальной энергии (Urot=0
), и единственный вклад в энергетические уровни даёт лишь кинетическая энергия вращения. В классической механике энергию такого движения можно было бы отождествить с энергией чисто тангенциального (касательного) перемещения частицы по сфере.
Смотрите также
Очистка металлов от вредных примесей
...
Расчет численности работающих.
Численность
трудящихся проектируемого объема рассчитывается по категориям и группам
работников: основные рабочие, вспомогательные рабочие (включая дежурный и
ремонтный персонал), инженерно-техничес ...
Биогенные амины и алкалоиды
К
пищевым заболеваниям относятся заболевания людей, возникающие при потреблении
продуктов питания с наличием в них опасных для человека микроорганизмов или
ядовитых веществ. Пищевые отравле ...