Элементы статистической термодинамики.
qV=Sexp[-(V+1/2){hn0/kT}]= ; gV=1
1) 
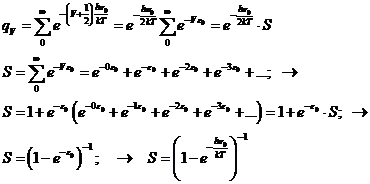
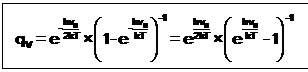
2) 
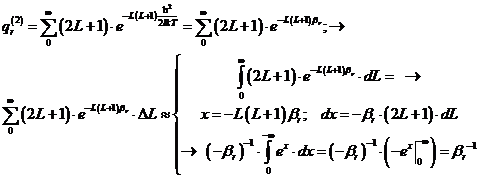
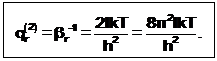
3) 
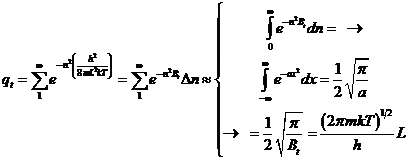
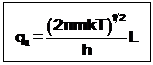
Лекция 17. Статистические суммы молекулярных движений и учёт симметрии. Свободная энергия, энергия Гиббса, уравнение состояния, химический потенциал, стандартизация. Стандартное сродство. Константа равновесия химической газовой реакции.
Началом отсчёта колебательной энергии удобно считать нулевой вибрационный уровень. Это связано с тем, что у простых двухатомных молекул экспериментально именно с основного колебательного уровня определяется энергия диссоциации, именно она является основой всех оценок прочности связи, а нуль вибрационной энергии просто-напросто запрещён принципом Гейзенберга. Он может быть определён только теоретически в качестве гипотетического минимума потенциальной кривой (кривой Морзе - адиабатического потенциала - энергетической кривой основного электронного терма молекулы (одной двухцентровой связи) в приближении Борна-Оппенгеймера).
1) Коррекция колебательной суммы состояний состоит в уточнении способа отсчёта энергии колебаний. Её лучше отсчитывать не от нуля, а от основного уровня (с V=0), которому отвечает остаточная энергия колебаний. Именно с этого уровня должна была бы происходить диссоциация химической связи в гипотетических условиях при абсолютном температурном нуле.
Вибрационные уровни энергии, отсчитываемые от уровня остаточных колебаний и вибрационная статистическая сумма определяются простейшими формулами:
Ev=vh0; → qv(ν0,T)=[1-exp(-hν0/kT)]-1.
Для каждой вибрационной степени свободы записывается своя собственная сумма состояний.
2) Коррекция вращательной суммы состояний состоит в учёте числа симметрии двухатомной гомоядерной молекулы A2:
qr(2)= 8pIkT/h¬s ®qr(2) = 8pIkT/sh
Эта приближённая формула qr(2) пригодна для молекулы линейной формы, у которой имеется две внешние ротационные степени свободы.
Для каждой вращательной степени свободы можно приближённо записать свою собственную сумму состояний qr(1), представляя её в виде квадратного корня из предыдущей величины, и это даёт
qr(1) = (8pIkT)1//h.
Было бы правильно различать внешние и внутренние вращательные степени свободы.
Обычно система уровней вращения молекулы определяются геометрической конфигурацией её ядерного остова. Существует несколько моделей такого распределения. Их называют волчками разных типов.
На основе квантовой механики для волчков различных типов невозможно получить общее аналитическое выражение ротационных сумм состояния.
Тем не менее, для этой цели существуют достаточно точные приближённые приёмы, основанные на классических способах описания вращения достаточно тяжёлых молекул с близко расположенными ротационными уровнями.
Смотрите также
Генеральный план. Пояснения к схеме
генерального плана.
Проектируемый цех расположен
на территории г. Казань.
Площадь для проектирования
цеха имеет ровную поверхность.
Производственные здания
расположены с учетом безопасных расстояний, санитарных ...
Создание и исследование шпаклевочных паст на основе УПС и АВС
...