Методы вывода кинетических уравнений
(2) 
(3) 
Согласно (19):
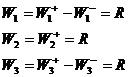
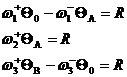
Имеем три уравнения и уравнение материального баланса 
, т.е. три уравнения с тремя неизвестными QA, QB и R. Заменив Q0 через 1, QA, QB, можно методом Крамера найти R.
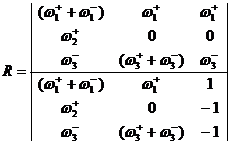
(38)
Преобразуем уравнение (38):
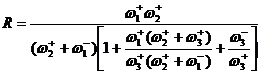(39)
Первый сомножитель в знаменателе – следствие квазистационарности процесса, второй сомножитель есть закомплексованность катализатора (следствие учета материального баланса по катализатору). Если стадия (2) является лимитирующей стадией, то 
и 
. Тогда,
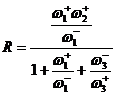(40)
(41)
В условиях квазиравновесия стадий (1) и (3) уравнение (41) можно получить, используя уравнение изотермы Ленгмюра:
и уравнение для скорости лимитирующей стадии 
.
Для одномаршрутных линейных механизмов удобно использовать уравнение Темкина, если скорость реакции записывать через свободную концентрацию активного центра ([М] или Q0):
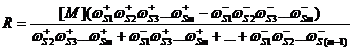(42)
Для рассмотренного выше примера 7:
(43)
Найдя из уравнения (43) Q0, из скоростей второй стадии QА и QВ из скорости стадии (3), можно также получить уравнение (38):
, 
и 
Сложив Qi, получим , найдем R.
Смотрите также
Расчет численности работающих.
Численность
трудящихся проектируемого объема рассчитывается по категориям и группам
работников: основные рабочие, вспомогательные рабочие (включая дежурный и
ремонтный персонал), инженерно-техничес ...
Электросинтез хлорной кислоты
...
Пятая группа периодической системы
По электронным структурам нейтральных атомов
рассматриваемая группа может быть разделена на две подгруппы. Одна из них
включает азот, фосфор, мышьяк и его аналоги, вторая — ванадий и его аналоги.
...