Квантовые числа. Атомные орбитали.

ms= +1/2; –1/2.

Оно получено из опытов Штерна и Герлаха.

Рассмотренные квантовые числа определяют энергию электрона, объем и форму пространства, в котором вероятно его пребывание в околоядерном объеме, т.е. размер, форму и ориентацию орбитали в пространстве.

Так как волновая функция y является решением уравнения Шредингера при всевозможных значениях квантовых чисел, то можно сказать, что волновая функция является в свою очередь функцией рассмотренных квантовых параметров n, l и ml, где:

n= 1, 2, 3, 4,…,

l= 0, 1, 2, 3,…,n–1

ml=–l,…, –1, 0, +1,…, +l

Атомные орбитали. Так как вероятность нахождения электрона в пространстве далеком от ядра очень мала, когда говорят об орбиталях, то имеют в виду такую область вокруг ядра атома внутри которой сосредоточено 90–95% электронного заряда. С точки зрения квантовой механики атомные орбитали являются геометрическим изображением волновой функции y (n, l, ml).

Z Электронное облако. Если бы в каждый момент времени

y определяли положение электрона в трехмерном пространстве и

ставили в том месте точку, то через множество таких определений

X получили бы картину в виде пространственного облака изображен-

ного точками с размытыми краями /рис.2.3.)

рис.2.3.

Такое зарядовое облако называют электронным облаком. Его плотность, пропорциональная y2, является непосредственной мерой вероятности нахождения электрона. Граничная поверхность облака, внутри которой содержится 90–95% электронного заряда, дает форму орбитали.

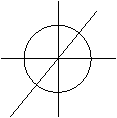Z s-орбиталь. Она существует при l=0. Значение ml тоже равно

Y нулю. Имеем только одно значение ml =0. Следовательно,

s-орбиталь имеет максимальную симметричность. У нее

X сферическая форма (рис.2.4.). В этом случае вероятность на–

хождения электрона в околоядерном пространстве определя–

рис.2.4. ется только радиусом-вектором и не зависит от угла координат.

y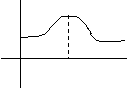 Радиальное распределение электронной плотности для 1s

электрона соответствует кривой с максимумом (рис.2.5.).

Максимум распространения вероятности находится на

0 r1 r,A0 расстоянии от ядра r1, которые соответствует радиусу

рис.2.5. первой боровской орбиты.

р-орбиталь. Существует при l=1. ml = –1, 0, +1.

Z р-орбиталь появляется на втором и всех последующих

Рz уровнях. Так как ml имеет три значения, то на р-подуров-

Y не каждого уровне может быть три р-орбитали. р-орбиталь

имеет гонтелеобразную форму. Все три р-орбитали распо-

X лагаются в пространстве по направлению координатных

Px осей. Их называют соответственно рх, рy, рz-орбитали

Py (рис.2.6.).

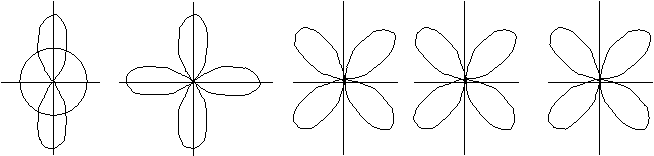Рис.2.6. Z Y Y Z Z

X X X X Y

dz2 dx2 y2 dxy dxz dyz

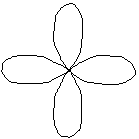
рис.2.7.

d-орбиталь. Появляется при l=2 на третьем квантовом уровне. На d-подуровне может быть уже пять различных состояний электронов, поэтому на d-подуровне каждого квантового уровня содержится пять d-орбиталей. В этом случае ml принимает пять значений: ml = –2, –1, 0, +1, +2, d-орбитали имеют более сложную форму, чем р-орбитали, они либо в виде четырех лепестков либо в виде гантели с ободком (рис.2.7.).

f-орбиталь. Появляется при значении l=3. f-орбитали могут быть только на четвертом и более отдаленных уровнях. Так как при l=3 ml имеет 7 значений /–3, –2, –1, 0, +1, +2, +3/, то на f-подуровне может быть семь орбиталей. Форма f-орбиталей еще более сложная, чем у d-орбиталей. f-орбитали изображают в виде сложных шестилепестковых фигур.

Copyright © 2025 - All Rights Reserved - www.chemicalnow.ru