5. Процессы. Второй закон термодинамики
уравнение Клаузиуса-Клапейрона, дифференциальная форма уравнения.
Уравнение устанавливает взаимосвязь между теплотой фазового перехода, давлением, температурой и изменением молярного объема.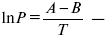 
эмпирическая форма уравнения Клаузиуса-Клапейрона.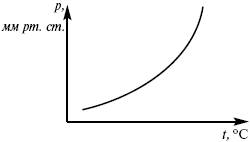 
Рис. 7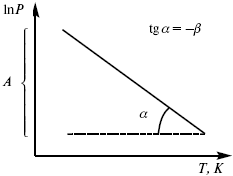 
Рис. 8
Уравнение Клаузиуса-Клапейрона изучает фазовые переходы. Фазовые переходы могут быть I рода и II рода.
I рода – характеризуются равенством изобарных потенциалов и скачкообразными изменениями S и V.
II рода – характеризуются равенством изобарных потенциалов, равенством энтропий и равенством молярных объемов.
I рода – ΔG = 0, ΔS ≠ 0, ΔV ≠ 0.
II рода – ΔG = 0, ΔS = 0, ΔV = 0.
Алгебраическая сумма приведенных теплот для любого обратимого кругового процесса равна нулю.
Эта подынтегральная величина – дифференциал однозначной функции состояния. Эта новая функция была введена Клаузиусом
в 1865 г. и названа энтропией – S (от греч. «превращение»).
Любая система в различном состоянии имеет вполне определенное и единственное значение энтропии, точно так же, как определенное и единственное значение Р, V, T и других свойств.
Итак, энтропия выражается уравнением: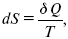 
где S – это функция состояний, изменение которой dSв обратимом изотермическом процессе перехода теплоты в количество Q равно приведенной теплоте процесса.
При независимых переменных U (внутренняя энергия) может обозначаться U ВН и V (объем), или Р (давление) и Н (энтальпия). Энтропия является характеристической функцией. Характеристические функции – функции состояния системы, каждая из которых при использовании ее производных дает возможность выразить в явной форме другие термодинамические свойства системы. Напомним, в химической термодинамике их пять:
1) изобарно-изотермический потенциал (энергия Гиббса) при независимых переменных Т, Р и числе молей каждого из компонентов и.;
2) изохорно-изотермический потенциал (энергия Гельмгольца) при независимых переменных Т, V, ni ;
3) внутренняя энергия при независимых переменных: S, V, ni ;
4) энтальпия при независимых переменных: S, Р, пi ;
5) энтропия при независимых переменных Н, Р, ni ..
В изолированных системах (U и V= const) при необратимых процессах энтропия системы возрастает, dS > 0; при обратимых – не изменяется, dS = 0.
Связь энтропии с другими термодинамическими параметрами
Для того, чтобы решить конкретную задачу, связанную с применением энтропии, надо установить зависимость между ней и другими термодинамическими параметрами. Уравнение dS = δQ/T в сочетании с δQ = dU + PdV и δQ = dH – VdP дает уравнения:
dU = TdS – PdV,
dH = TdS + VdP.
Записав уравнение: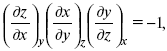 
применительно к функциональной зависимости φ(Т, V, S) = 0, получим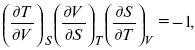 
т. е.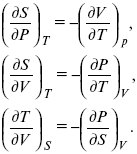 
Теперь найдем зависимость энтропии от температуры из уравнений: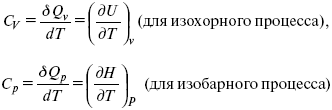 
и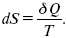 
Вот эти зависимости: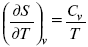 
и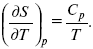 
Смотрите также
Каучуки
Каучуки — натуральные или
синтетические материалы, характеризующиеся эластичностью, водонепроницаемостью
и электроизоляционными свойствами, из которых путём специальной обработки
получают р ...
Характеристика исходного сырья
Добываемая из скважин эмульсия
представляет собой многофазную систему, состоящую из нефти, пластовой воды и
попутных нефтяных газов. Нефть представляет собой химически сложную компонентную
смесь, ...
Возможная схема этапов оптимизации ХТС
Процессы
химической технологии это сложные физико-химические процессы, протекающие как в
пространстве, так и во времени. В них участвуют потоки энергии (тепло и холод)
и многофазные и много ...