Однородные функции. Уравнение Гиббса-Дюгема.
Функция многих переменных, например F(x,y,z), называется однородной функцией порядка k, если она обладает следующим свойством:
F (tx, ty, tz) = tk F (x, y, z),
(например, F = x3 +x2y + y2x + z3 является однородной функцией 3-его порядка). Однородные функции обладают следующим свойством (теорема Эйлера): 
.
Доказательство теоремы Эйлера следующее:
Если f = f (x1, x2,…xn ), а каждое xi = φ(t), то 
.
Пусть F (x, y, z ) - однородная функция порядка k, положим x = tα, y=tβ, z = tγ, тогда 
.
Продифференцируем по t: 
.
Положим t = 1,тогда α = x, β = y, γ = z и 
, что и требовалось доказать.
Если температура и давление постоянны, то энергия Гиббса является функцией только числа молей компонентов: G = G (n1, n2, …nk ) и легко сообразить, что она является однородной функцией первого порядка относительно числа молей компонентов и по теореме Эйлера (k = 1):
.
После дифференцирования имеем: 
.
Но 
, а при p, T =const 
.
Следовательно, 
.
Это уравнение называется уравнением Гиббса-Дюгема и широко применяется в термодинамике растворов поскольку дает возможность рассчитать dμi i –ого компонента, если известны изменения химических потенциалов всех остальных компанентов в изобарно-изотермическом процессе. Для бинарного раствора 
.
Разделив на сумму п1 +п2, получим: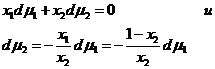 
.
Смотрите также
Винилхлорид - строение, свойства, получение и применение
Винилхлори́д (хло́ристый вини́л, хлорвини́л,
хлорэтиле́н, хлорэте́н, этиленхлори́д) — органическое вещество; бесцветный газ со слабым сладковатым
запа ...
Заключение
В заключение
курсового проекта можно сказать, что в процессе его создания были выполнены следующие
цели:
·
изложены основные концепции появления и ...
Химия гидразина
Химия гидразина изучается уже почти три четверти века. До 1875 г. были известны только симметричные дизамещенные гидразина— гидразосоединения. В 1875 г. Э. Фишер, исследуя процесс восстановлен ...