Линейное движение на ограниченном интервале (потенциальный ящик).
Эта задача простейшая. Частица, движущаяся на прямолинейном интервале между двумя идеально отражающими стенками, претерпевает абсолютно упругие удары об эти стенки и отражается, изменяя лишь направление вектора скорости (импульса). Модуль же сохраняется. Возникает поступательное строго периодическое движение с постоянной скоростью. Эта модель предельно идеализированная.
Полная энергия этой частицы содержит только кинетическую составляющую. Потенциальная энергия для простоты принята равной нулю. На отрезке пути укладывается целое число полуволн Де-Бройля. Это условие, из которого вытекает квантование (дискретность) модуля импульса и энергии.
Дискретные значения полной энергии называются энергетическими уровнями или просто уровнями. Множество уровней называется энергетическим спектром данной системы. Графическое изображение энергетических уровней в масштабе называется энергетической диаграммой.
Квантование энергии и энергетическая диаграмма частицы в одномерном "ящике" получаются из следующих вычислений.
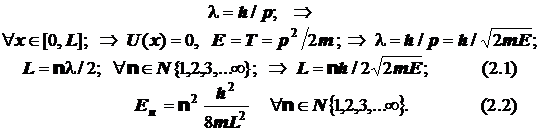
Смотрите также
Эволюционная химия
Тема
моего реферата: «эволюционная химия – высшая ступень развития химических
знаний». В нем будут рассмотрены вопросы, касающиеся места и роли химии в современной
цивилизации, задачи, конц ...
Билеты по химии органика и неорганика
...
Химия гидразина
Химия гидразина изучается уже почти три четверти века. До 1875 г. были известны только симметричные дизамещенные гидразина— гидразосоединения. В 1875 г. Э. Фишер, исследуя процесс восстановлен ...