Качественные сведения о химической связи
Нормировочный множитель: 
, (1)
Уровни энергии МО:
, (2)
Матричные элементы гамильтониана в выбранном базисе АО появляются из формулы энергии 
,
где удобно ввести обозначения:
- диагональные матричные элементы: 
и
- недиагональные матричные элементы: 
Отсюда компактная формула для энергии 
, (3)
Раскрываем слагаемые матричных элементов гамильтониана:
а) диагональный матричный элемент:
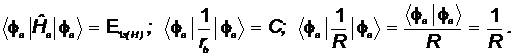
б) недиагональный матричный элемент:
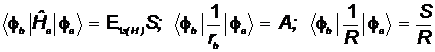
Окончательно формула для энергии приобретает вид:
, а.е. (4)
Энергия выражена через одноэлектронные молекулярные интегралам:
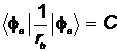- кулоновский интеграл
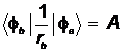- обменный интеграл
- интеграл перекрывания. (5)
Молекулярные орбитали имеют вид (для графического вывода):
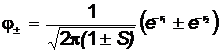. (6)
Для количественных расчётов необходимы
Двухцентровая система координат. Эллиптические переменные.
.
Вычисление слагаемых энергии:
1) Уровень исходной базисной АО 
2) Интеграл перекрывания:
.
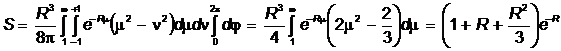3) Кулоновский интеграл:
,
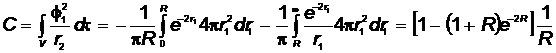4) Резонансный интеграл:
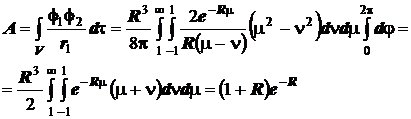
При подстановке выражений этих молекулярных интегралов в формулу для энергетических уровней ( ), получаются энергетические уровни МО 
в явном виде, выраженные в зависимости от межъядерного расстояния.
Результаты простейшего расчёта, полученные с применением водородных 1s-АО следующие:
Эксперимент даёт:
.
В количественном отношении простой подход МО ЛКАО неудовлетворителен и требуется его уточнение. Необходимо улучшить физическую модель.
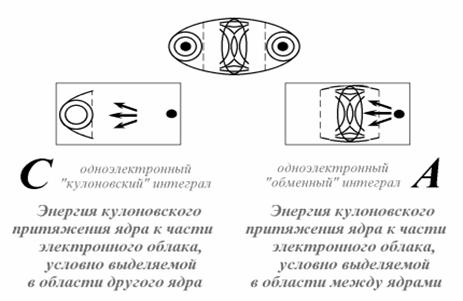
Качественная интерпретация одноэлектронных молекулярных интегралов:
Смотрите также
Расчет проектной себестоимости продукции.
В
курсовом проекте в зависимости от характера продукции, выпускаемой
проектируемым объектом, рассчитывается ее полная или производственная
себестоимость, или внутрицеховые затраты по данному переде ...
Влияние химических веществ на здоровье человека
Международное
изучение последствий подвергания диоксинам и неопухолевой смертности рабочих по
производству и распылению кислородо- и фенолосодержащих гербицидов и хлорофенолов.
...
Ассортимент, качество и состав тяжелых видов моторных топлив
Стандарт на котельное
топливо — ГОСТ 10585—75 предусматривает выпуск четырех его марок: флотских
мазутов Ф-5 и Ф-12, которые по вязкости классифицируются как легкие топлива,
топочных мазу ...