Соотношения неопределённостей Гейзенберга
7.2.5.2. Если коммутатор 
ненулевой, то получаемая информация зависит от последовательности измерений, и величины и в одном приборе в принципе совместно не могут быть измерены.
Что же имеет место в природе на самом деле? Попробуем получить ответ.
7.3.Соотношения неопределённостей Гейзенберга.
7.3.1. Накоплена достаточная информация, чтобы решить одну из важнейших проблем квантовой механики, связанную с совместными измерениями динамических переменных.
Исследуем, можно ли измерить:
- импульс частицы, находящейся в определённой точке пространства;
- момент импульса вращающейся частицы в определённой точке орбиты;
- энергию системы в конкретный момент времени.
7.3.2. Выбор этих пар динамических переменных не случаен. Эти пары величин взаимно дополняют друг друга таким образом, что их произведение обладает размерностью циклической константы Планка 
, так что 
.
Размерность величины 
является произведением размерностей энергии и времени или импульса и расстояния. Физическую величину с такой размерностью принято называть действием. В силу этого-то константу Планка часто называют квантом действия.
7.3.3. Образуем три коммутатора 
, 
, 
, необходимых для исследования этих трёх ситуаций согласно выводам предыдущих параграфов. Сразу же запишем выражения и для комплексно сопряжённых операторов.
7.3.4. Первый коммутатор построим из оператора компоненты импульса и соответствующей ему координаты:
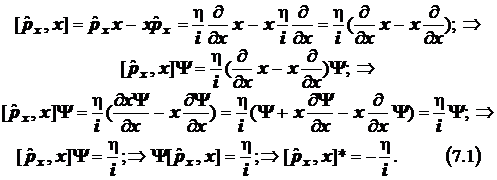
7.3.5. Второй коммутатор построим аналогично из оператора момента импульса и ему соответствующей координаты - угла поворота плоского ротатора:
.
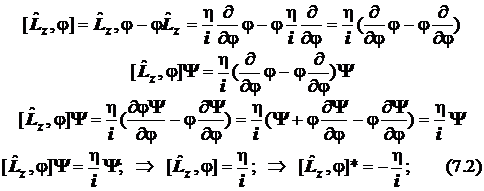7.3.6. Также и третий коммутатор построим из оператора энергии и времени. Зависящий от времени гамильтониан заимствуем из временного уравнения Шрёдингера:
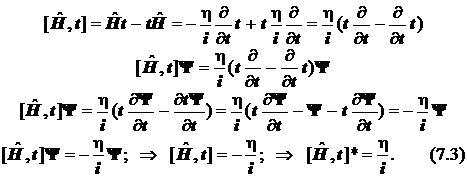
Перед Вами наиболее последовательный операторный вывод соотношений неопределённостей Гейзенберга. Они относятся к числу фундаментальных законов природы.
7.3.7. Все три коммутатора не равны нулю, и их численные значения мнимые и равны либо
, либо -
. Вместо мнимых значений удобно построить на их основе действительные квадраты модулей. Для этого каждое из полученных мнимых значений умножается на комплексно сопряжённую величину. Полагая волновую функцию нормированной, для компоненты импульса и соответствующей координаты получаем равенства:
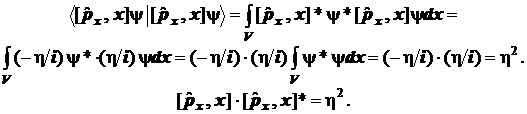
Квадрат модуля каждого из трёх коммутаторов один и тот же. Во всех случаях получается 
. Во всех случаях получается квадрат циклической константы Планка:
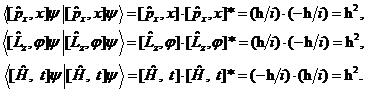(7.4)
7.3.8. Это значение получено наиболее строго и представляет собою среднеквадратичный разброс, теоретически предопределённый для любого эксперимента, нацеленного на совместное измерение пар динамических переменных.
Разброс порядка величины константы Планка для явлений микромира очень велик - настолько велик, что совместные количественные измерения динамических переменных с таким коммутатором лишены физического содержания.
Так в определённой точке линейной траектории невозможно точно указать величину импульса системы, и, напротив, при точно фиксированном импульсе системы невозможно указать её точное положение.
В определённой точке траектории криволинейного движения невозможно указать вектор момента импульса, но если момент импульса фиксирован, то нельзя указать положение тела на криволинейной траектории.
В точно определённый момент времени невозможно указать энергию движущегося тела, и напротив, точное определение энергии тела не может быть привязано к определённому моменту времени в эволюции системы.
Смотрите также
Кобальт
...
Технология неконцентрированной азотной кислоты
Азотная
кислота по объему производства занимает среди других кислот второе место после
серной кислоты. Все возрастающий объем производства HNO3
объясняется огромным значением азотной кислот ...