Движение частицы на круговой орбите.
В этой задаче вычисления так же достаточно идеалистичны, как и в предыдущей.
Физическое содержание задачи в дальнейшем неизбежно многократно обсуждается с различными смысловыми вариациями, но для этого начинающему нужна хотя бы предварительная количественная основа. Так меня учили .
Поэтому наша цель вначале не в строгости, а в возможности пусть и эклектического, "лоскутного", в какой-то мере живописного, но всё же количественного описания. Строгость выводов - потом. Итак, поскорее к цели .
Если частица движется по кругу в поле центральной кулоновской силы, создаваемой ядром с порядковым номером Z, то на замкнутой "круговой орбите" укладывается целое число волн материи 2r=n/2, "nÎN{1,2,3, .}. Следует вывод о том, что квантованной оказывается величина, похожая на модуль момента импульса: =Vr = n(h/2), "nÎN.
В качестве такого водородоподобного атома следует рассматривать многозарядный ион, у которого оставлен всего один электрон. Можно так же рассматривать и атом позитрония. Это электрон-позитронная пара до аннигиляции .
Центростремительная сила, удерживающая частицу на круговой орбите, имеет кулоновскую природу, и из баланса этих сил получается "теорема вириала", определяющая взаимосвязь между кинетической и потенциальной энергиями в поле центральной силы 2T=-U. По этой теореме кинетическая энергия равна половине потенциальной, но с положительным знаком, а полная энергия равна половине потенциальной E=U/2 и также отрицательна E=-Ze2/2r. Простейшие расчёт показывают, что возможные значения радиуса классической "орбиты" дискретны – квантованы r=(n2/Z)(h/2)2/(mee2). Соответственно квантованы и значения полной энергии. Результирующее выражение для дискретных энергетических уровней называется формулой Бора.
Приведём всю сводку вычислений, а комментарий к ним только что был дан выше:
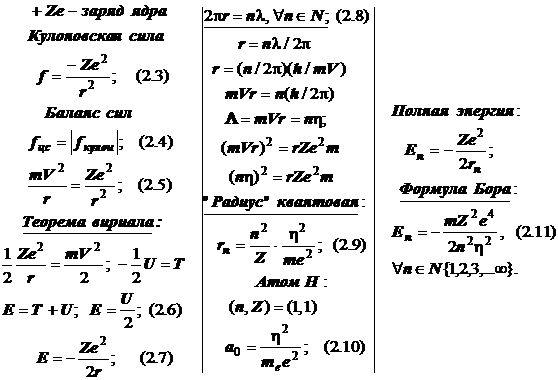
Для корректных расчётов свойств системы, состоящей из двух взаимно обращающихся частиц с конечными массами следует использовать общую приведённую массу. Приведённая масса системы электрона и протона учитывает их обращение вокруг общего центра масс и мало отличается от массы электрона. Она равна
= eMp /( e+Mp)=1840/1841
Введя приближение e<<Mp , можно принять =e.
Формула Бора и выражение для боровского "радиуса" корректно выводятся из решения уравнения Шрёдингера для атома H. Квантово-механический вывод логически строен, но это достигается за счёт резкого усложнения математической стороны задачи. Величина a0=0.529 Ao называется боровским радиусом. В полуклассической квантовой теории он считается радиусом первой круговой орбиты, на которой электрон движется в основном квантовом состоянии, но эта примитивная картина неверна и её содержание будет изменено в квантовой механике. Её истинный смысл вероятностный. Он выявляется лишь из квантово-механического анализа свойств атома H. Боровский радиус есть не что иное, как расстояние наиболее вероятного удаления электрона от ядра на низшем энергетическом уровне - в основном состоянии атома.
Смотрите также
Генеральный план. Пояснения к схеме
генерального плана.
Проектируемый цех расположен
на территории г. Казань.
Площадь для проектирования
цеха имеет ровную поверхность.
Производственные здания
расположены с учетом безопасных расстояний, санитарных ...
Металловедение
Металловедение – наука,. Изучающая строение
и свойства металлов и устанавливающая связь между их составом, строением и
свойствами.
В данном реферате приведены общие и
теоретические сведе ...