Методика расчёта колебательных спектров и представление результатов.

В N-атомных системах все ядра совершают свои собственные гармонические колебания, любое из этих колебаний, как известно, можно представить в виде суперпозиции нормальных колебаний, которые выглядят следующим образом:

Qi =Qi0sin((li)½t + di), (34)

и частота равна

ni=(1/2p)(li)½, (35)

такое колебание называется нормальным колебанием, где Qi называются нормальными координатами системы. В общем случае для N-атомной нелинейной молекулы число нормальных колебаний равно 3N-6, а для линейной N-атомной молекулы 3N-5, т.к. у такой молекулы отсутствует вращательная степень свободы. Таким образом, общая форма молекулярного колебания является суперпозицией 3N-6 (или 3N-5) нормальных колебаний, описываемых формулой выше приведённой формулой. Физический смысл нормальных колебаний заключается в следующем, следует, что при нормальном колебании все ядра совершают движение в одной и той же фазе и с одинаковой частотой.

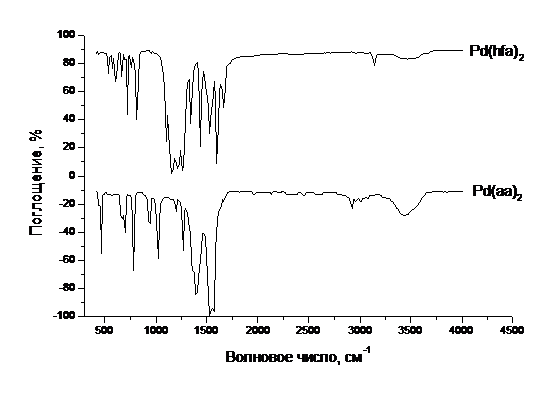
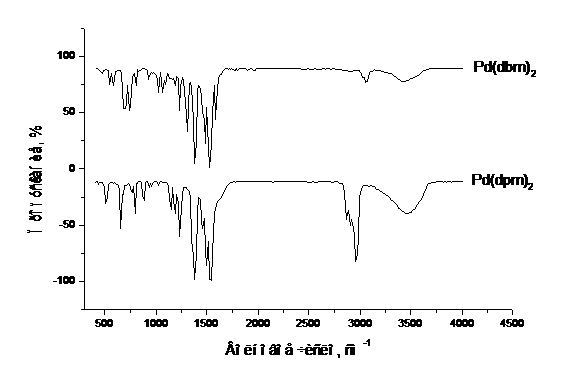
Рис.1. Спектры ИК-поглощения b-дикетонатов палладия (II) в диапазоне 400-4000 см-1.

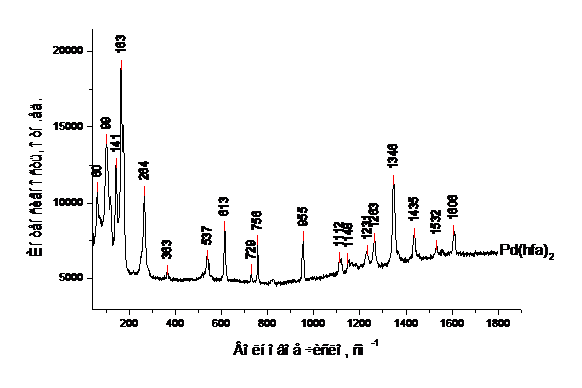
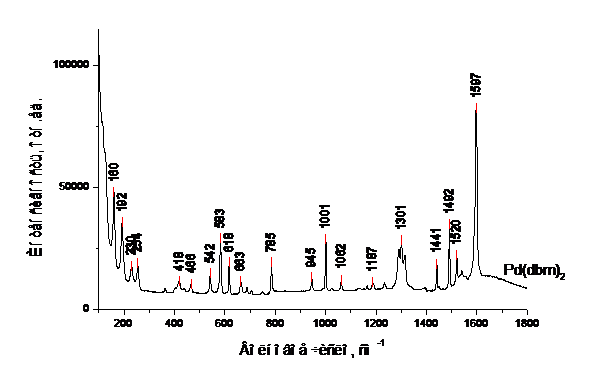
Рис.2. Спектры КР кристаллической фазы b-дикетонатов палладия (II).

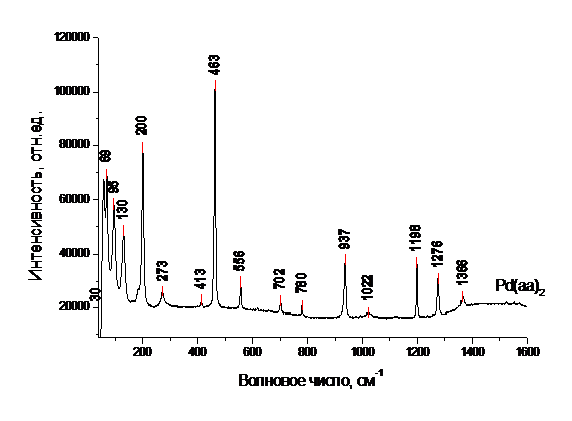
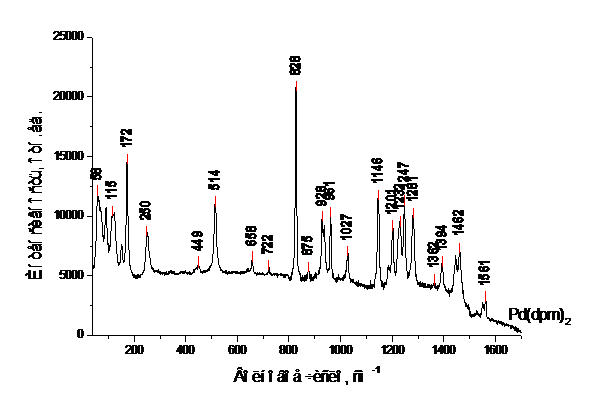
Рис.3. Спектры КР кристаллической фазы b-дикетонатов палладия (II).

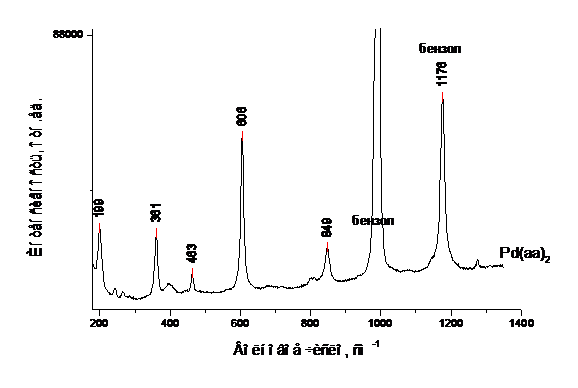
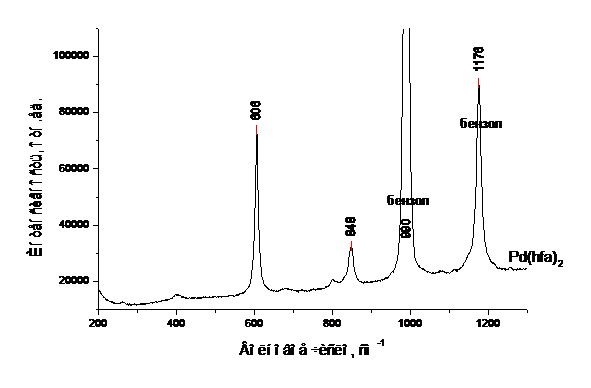
Рис.4. КР спектры растворов b-дикетонатов палладия (II) в бензоле.

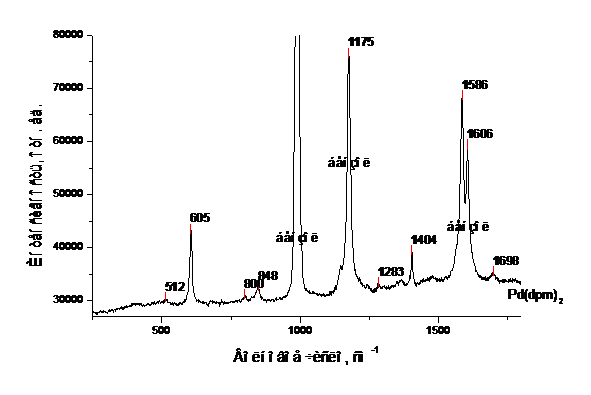
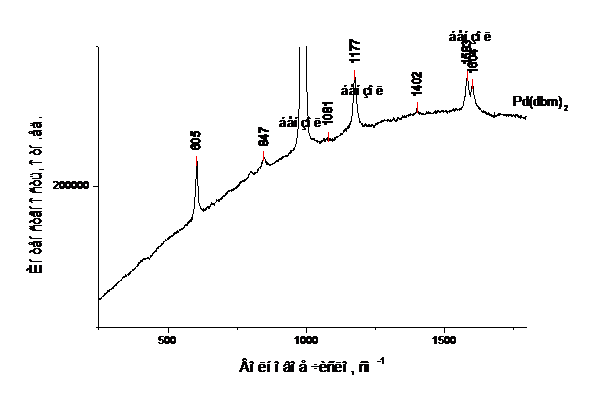
Рис.5. КР спектры растворов b-дикетонатов палладия (II) в бензоле.

Как указывалось выше, частота нормального колебания определяется кинетической и потенциальной энергией системы. Кинетическая энергия определяется геометрическим расположением отдельных молекулы системы и их массой. Потенциальная же энергия характеризует взаимодействие между отдельными атомами и записывается в виде функции силовых постоянных. Знание потенциальной энергии позволяет получить достаточную информацию о природе сил, действующих между атомами. Это возможно лишь при наличии силовых постоянных, полученных из наблюдаемых частот. Эту задачу решают вычислением частот в предположении ряда соответствующих силовых постоянных – прямая колебательная задача. Если между вычисленными и наблюдаемыми частотами имеется удовлетворительная корреляция, то соответствующий ряд силовых постоянных рассматривают как представление потенциальной энергии исследуемой системы. Для вычисления частот колебаний нужно, прежде всего, выразить потенциальную и кинетическую энергии через какие-либо общие координаты, таковыми являются внутренние координаты.

Они характеризуют изменения межатомных расстояний и валентных углов, тем самым силовые постоянные приобретают более ясный физический смысл, чем при использовании прямоугольных координат, т.к. эти силовые постоянные являются характеристиками изменений валентных угла и связи. В набор внутренних координат не входят координаты, описывающие поступательное и вращательное движения молекулы как целого.

При уточнении силовых постоянных по экспериментальным частотам (обратная спектральная задача – ОСЗ). В отличие от прямой задачи, ОСЗ может не иметь единственного решения. Такая задача является математически не корректной из-за чувствительности результатов к заданию экспериментальных данных, большого числа искомых переменных и плохой обусловленности решаемых уравнений. При постановке ОСЗ в математически определённой форме, кроме частот колебаний, привлекались дополнительные экспериментальных данные: колебательные спектры ближайших членов гомологического ряда.

В приближении обобщённых валентных сил, кроме силовых постоянных валентно-силового поля, вводят недиагональные силовые постоянные взаимодействия валентных координат. Это приближение является наиболее распространённым и близким по смыслу к химическим представлениям о межатомных силах.

В приближении обобщённого валентно-силового поля потенциальная энергия нормального колебания n выражается в виде: